TOLERANS ÖLÇÜ ORANLARI
Ölçüsel uzlaşmalar yapı işlerinde eski zamanlardan bari kullanışa gelmiştir. Gerçek sayılar Pisagor zamanından kalmıştır. Pisagor, akustik sayı oranlarının optik armonik olması gerektiğinden yola çıkmıştır. Bu şekilde, bütün uyumlu boşluk orantılarını içeren fakat uyumsuz boşluktan saniye ve septimleri kapsamayan Pisagor hesap tekniği ortaya çıkmıştır.
Bu sayı oranlarından boşluk ölçümleri oluşmuştur. Pisagorik veya diofantik denklemler alnın genişlik, yükseklik ve uzunluğunda kullanılan sayı guruplarını 2,3,4, oluşturmuştur.
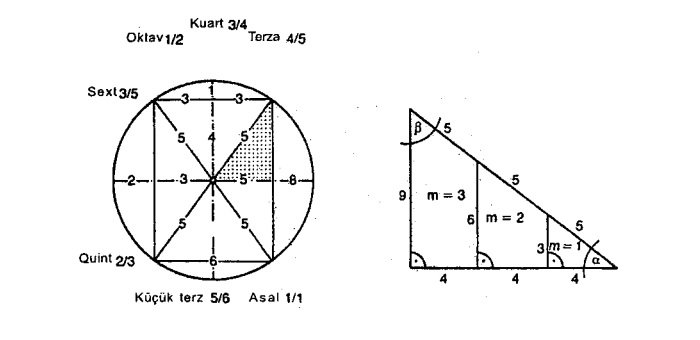
a2+b2=c2 formülü ile bu sayı grupları hesaplanabilir.
a2+b2=c2
a = m (y2- x2)
b=m.2.x.y
c = m (y2 + x2)
Burada: x, y: Bütün rakamlar
x küçüktür y'den
m: Büyültme veya küçültme faktörü
Platon ve Vitruv tarafından da sözü edilen Çember, Üçgen ve Kare gibi geometrik formlar büyük anlam taşımaktadır.
Bunlardan poligon dizisinin konstrüksiyonu çıkarılabilir. Diğer poligon dizimleri (öm. yedigen, dokuzgen) birleştirme veya üst üste konulma ile oluşturulabilir. Bu şekilde örneğin on beş gen, eşkenarlı üçgenin beşkenarla üst üste konması ile teşkil edilebilir. Beşgen veya düzenli beşgen yıldız (Druden ayağı) ve bundan meydana gelen on genin altın kesiti ile doğal alakası vardır. Fakat bunun tam ölçü oranları önceleri kullanılamazdı. Dairesel" yapıların tasarımı ve konstrüksiyonu için poligon dizimi gerekir.
TOLERANS ÖLÇÜ ORANLARI ESASLARI
Taban çizgisi ile yükseklik arasındaki oranı 1:2 olan eşkenar dik üçgen bir kare ile orantılıdır. Taban ve yüksekliği kareye eşit olan bir eşkenar üçgeni, Dom inşaat mimari Knauth Strassburg Dom'unun ölçü oranlarının hesaplanmasında kullanmıştır.
A.v. Drach'ın p/4 üçgeninin yüksekliği çevrilen karenin ucu tarafından tayin edildiğinden, öngörülene nazaran biraz sivridir. Kaşifi tarafından ayrıntılarıyla başarılı bir uygulama ile cihazlarda denenmiştir. Bu figürlerin yanı sıra sekizgenin ölçü oranları L.R. Spitzenpfeil'in araştırmalarında eski yapı örneklerinde gösterilmiştir. Esas olarak burada bilinen diyagonal üçgen alınmıştır. Üçgen yüksekliği burada yarım ana çizgi üzerinden teşkil edilen karenin diyagonalıdır.
Bu şekil teşkil edilen dikdörtgenin kenar oranı 1/√2dir. Buna göre, bütün dikdörtgenlerin bölme veya çarpımları aynı kenar oranına eşittir 1/√2dir. Bundan dolayı bu ölçü oranı Dr. Porstmann tarafından Alman DIN formatına esas teşkil edilmiştir. Buna ilişkin geometrik seriler sekizgenin dahilinde basamakları verir.
Çarpanlara ayırma işlemi bir yapıdaki dikey olmayan yapı parçalarının kare köklerinin kullanımını mümkün kılmaktadır. Mengeringhausen MERO kare sayılarının yaklaşık oranlarının yardımıyla oda çatı makaslarını geliştirmiştir. Prensip ise bilinen "salyangoz" dur.
Sağ köşenin noksanlığı çubukların vida bağlantıları vasıtası ile atılan düğümle dengelenmiştir. Bütün sayıların kare köklerinin farklı tahmini hesapları √n dikey olmayan yapı parçaları için G Form'unda zincir kesirini vermektedir. G Formu =
√n=1+ (n-1)/(1+G)
TOLERANS ÖLÇÜ ORANLARI ESASLARI KULLANILIŞI
Geometrik ve ölçü ilişkilerinin yukarıdaki veriler esasında kullanımını Vitruv göstermektedir. Onun araştırmalarına göre örn. Roma Tiyatrosu dört defa döndürülen üçgen üzerine, Yunan Tiyatrosu üç defa döndürülen kare üzerine yapılmıştır. Her iki konstrüksiyon onikigeni verir. Merdiven girişlerinde bu tespit edilebilir. Altın kesit esasına dayanan ölçü oranları ile Moessel fazla inanılır olmasa bile, bunu ispatlamak istemiştir. Zemin planı, beşgen üzerine oturtulmuş tek Yunan Tiyatrosu, Epidauros'dadır.
Roma'nın eski bir limanı olan Antia Ostia'da bulunan yerleşme alanında kutsal kesitin taslak prensibi ortaya çıkarılmıştır. Bu prensip bir karenin diyagonalinin yarıya bölünmesini esas almıştır. Daire yaylarının bir karenin kenarlarını kestiği noktalar birleştirilirse 9 parçalı bir kafes oluşturulur. Ortadaki kare altın kesitin karesidir. AB yayının, ikiye bölünmüş esas karenin CD diyagonali gibi uzunluktaki yüzde 0,6 toleransı vardır.
Bundan dolayı altın kesit çemberin kareye oranlanması için yaklaşık metodunu oluşturur. Temel planından itibaren inşaat ayrıntılarına kadar tüm genel yapı kompleksi işte bu ölçü oranları ile yapılmıştır.
Palladio'nun 4 kitabında, Pisagor'un verileri üzerine oluşan mimarlık için geometrik anahtarlar sunulmaktadır. O da aynı alan ilişkileri (çember, üçgen, kare v.s.) ve kendi yapısı için armonileri kullanmaktadır. Son derece açık olarak formüle edilmiş kurallara Doğu'nun eski kültür halklarında rastlanır. Bu şekilde, Hintliler kendilerinin "Manasara"sını, Çinliler "Toukou" ile ilgili modülasyonunu, Japonlar da kendilerinin "Kiwariho" metodunu, oluşturarak geleneksel gelişmelerini sağlamış ve büyük çapta ekonomik faydalar elde etmişlerdir. 18 yüzyılda ve sonraları harmonik olmayan artan ölçü sistemi tercih edilmiştir. Buradan Oktametre sistemi geliştirilmiştir. Modül sisteminin uygulanmasıyla birlikte harmonik ve orantılı ölçüler tekrar işlev kazanmıştır. Koordinasyon sistemi ve koordinasyon ölçülerine ilişkin veriler mevcuttur.
18 yüzyılda ve daha sonraları armonik değil, toplama ölçü sistemi tercih edilmiştir. Buradan Oktametre sistemi geliştirilmiştir. Modül sisteminin uygulanmasıyla birlikte armonik ve orantılı ölçü ilişkileri tekrar işlev kazanmıştır. Mimar Le Corbusier, altın kesit ve insan vücudunun ölçüleri üzerine kurulan bu orantıyı geliştirmiştir. Bir mesafenin "altın kesiti" ya geometrik olarak ya da formüllerle ortaya çıkarılabilir. Bir mesafenin, buyüğe olduğu gibi küçüğe de aynı orantıyı sağlayacak şekilde bölünmesine "Altın kesit" denir. Kare, çember ve üçgen arasındaki ki orantı ilişkisini gösterir. Bir mesafenin altın kesiti zincir kesin ile de bulunabilir. Le Corbusier. Fibonacci'nin altın kesit dizilişini oluşturan insan vücudunun 3 aralığını belirlemiştir : ayak, karın boşluğu ve yukarıya doğru kaldırılan ellerin parmakları. Le Corbuser bir Avrupalıların ortalama boyunu = 1,75 m olarak ele almıştır. Bunu Le Corbusier altın kesite göre 108, 2-66. 8-41, 45-25,4 cm gibi ölçülere bölmüştür. Son ölçü pratik olarak 10 inç'e eşit olduğundan bu şekilde İngiliz inç ilişkisini ortaya çıkarmış, buna karşın yüksek ölçülen ortaya çıkaramamıştır. Le Corbusier, 1947 senesinde altın kesit yardımıyla tersine yukarıya ve aşağıya doğru kızıl hat oluşturmuştur. Bu dizilerin basamakları pratik kullanım olarak çok büyük olduğundan, 2,26 m'den yola çıkarak (kalkık elin parmak uçları) kırmızı hattın çifte oranını veren mavi hattı oluşturmuştur. Le Corbusier, kırmızı ve mavi hatların oranını pratik olarak kullanılabilir bir ölçüye oturtmuştur.
Etiketler : tolerans ölçü oranları